분류 평가
지도학습 중 이산변수인 category (class) 예측에 대한 평가 지표를 정리한다.
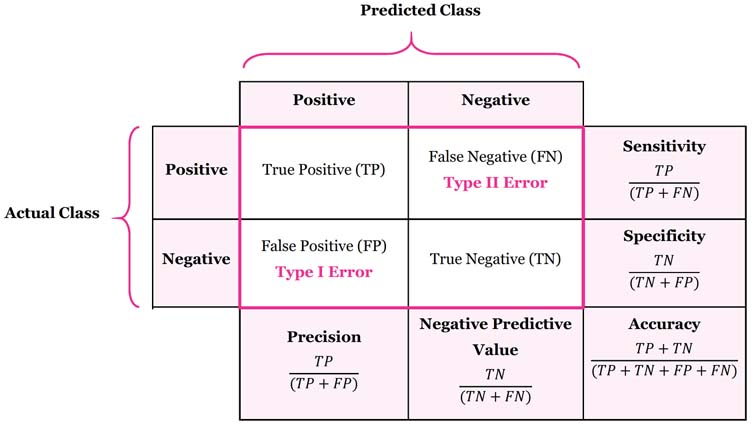
위 표는 confusion matrix 라는 것인데, actual class는 답, predicted class는 예측값이다. positive는 질병의 발병 등 무언가 중요한 사건을 말한다. TP와 TN는 모두 답을 맞춘 경우고, 그 외는 error로서, type I은 FP, type II는 FN이다. 즉, type I은 실제는 negative인데 positive로 잘못 예측한 경우이다. 예를 들어 질병이 없는데 질병이 있다고 예측한 것이다. type II는 실제는 positive인데 negative로 잘못 예측한 경우이다. 특히 이런 진단의 문제는 type II 오류를 늘리는 한이 있더라도(병이 있는데 병이 없다고 진단) type I 오류를 줄이는 과소 진단을 하도록 진단의 threshold를 높이는 것이 더 전체적 손실(인명손실)을 줄이는 방법일 것이다. 예를 들어 폐암이 없는데도 x-ray 사진 상 나타난 소견만으로 [낮은 threshold] 폐암이 있다고 진단을 하여 [type I error] 폐엽을 절제하는 수술을 하였는데 실제로는 폐암이 아닌 경우 이러한 과대치료에 대한 보상은 어떻게 하더라도 이 수술을 돌이킬 수가 없기 때문이다.
데이터 내에 예를 들어 금융위기나 암과 같이 드문 사건에 대한 샘플이 그렇지 않은 경우보다 상당히 적은 경우를 imbalanced dataset이라고 한다. 이 경우 accuracy만 보면 분류문제의 성과 평가를 제대로 할 수 없다. 통상 우리는 TP에 초점을 두는데, 이를 위해 sensitivity (=recall, TPR, true positive rate) 와 precision 을 측정하고, 그 상충관계를 모두 고려하기 위해 f1이라는 두 지표의 조화평균값을 함께 본다 (참고로, FPR는 1 - specificity로, FP / (FP+TN) 이다). 이 산식을 TP를 중심으로 해석해 보자면, precision은 TP + type I error 중에서 TP가 차지하는 비중, sensitivity (=recall) 는 TP + type II error 중에서 TP가 차지하는 비중이다.


ROC curve는 TPR를 종축, FPR를 횡축으로 그린 것이다 (구글 정의: An ROC curve (receiver operating characteristic curve) is a graph showing the performance of a classification model at all classification thresholds [2]). 이는 각각의 threshold별로 얻을 수 있는 (FPR, TPR) 조합을 좌표평면에 그린 것인데, 더 나은 분류모형 일 수록 TPR는 1, FPR은 0에 근접한다. 이는 즉, type I, type II error가 0인 모형이다.
[1] https://manisha-sirsat.blogspot.com/2019/04/confusion-matrix.html
[2] https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc